Volume 1 - the golden ratio
The Golden Ratio
Somewhere between watching a late night art documentary on Netflix and falling asleep in math class, many of us have probably heard of "The Golden Ratio" (not to be confused with "The Golden Rule"...totally different). Usually, not to far behind is the "Fibonacci Sequence" (FEE-BOW-NACHEE) which loves to pop up in math-related movies and plenty of sci-fi/mystery novels. Aside from making you sound educated and artistic in casual conversation, what's the big deal with these two? How are they related to each other, and how can they be used to improve or refine your designs? Let's start with the basics: What is the Golden Ratio?
From zero to infinity
To understand where the Golden Ratio comes from, we must first understand the Fibonacci Sequence. At its core, the sequence is simply "a set of numbers that starts with a one or a zero, followed by a one, and proceeds based on the rule that each number (called a Fibonacci number) is equal to the sum of the preceding two numbers". Well, that sounded fancy. Just bear with me here, it goes like this:
0 + 1 = 1
1 + 1 = 2
1 + 2 = 3
2 + 3 = 5......etc.
This pattern goes on infinitely, and if you omit the sums and just make note of the resulting numbers you end up with this list: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...etc, thus creating the "Fibonacci Sequence"! Now this is where it starts to get interesting ("starts to??!"...I know, I know, I've had you on the edge of your seat this whole time!). If we take this sequence and begin to divide each number by it's preceding number we start to notice a pattern:
2 ÷ 1 = .5 21 ÷ 13 = 1.615
3 ÷ 2 = 1.5 34 ÷ 21 = 1.619
5 ÷ 3 = 1.67 55 ÷ 34 = 1.618
8 ÷ 5 = 1.6 89 ÷ 55 = 1.618
13 ÷ 8 = 1.625 144 ÷ 89 = 1.618
As the numbers get larger, the answers all start to approximate the same number: 1.618. This is true no matter how high up the sequence you go as along as the two numbers are consecutive. It is this very number, the proportion that describes any two consecutive numbers in the Fibonacci Sequence, that we commonly refer to as "The Golden Ratio".
The Divine Proportion
Taking this ratio one step further, you can derive a rectangle where side x is equal to 1 and side x + y is equal to 1.618, known as a "Golden Rectangle":
You'll notice that in the above picture, both the larger rectangle (the pink square + the green rectangle), and the green rectangle alone can be considered Golden Rectangles as they share the same 1:1.618 ratio. If we continue to subdivide the smaller rectangle into further Golden Rectangles we get something that looks like this:
Now if we create a spiral that crosses through each of these rectangles we end up with...you guessed it, the "Golden Spiral"!
As the spiral grows, it gets wider every 1/4 turn by a factor of 1.618 commonly denoted by the Greek letter Phi (φ).
So why do these shapes matter? Well, it wasn't long after these proportions were discovered that people started to see them occurring naturally everywhere! We can witness this ourselves by taking a close look at the growth pattern of many plants and ferns, the incredibly efficient arrangement of sunflower seeds, the incremental growth of the nautilus shell, the proportions of the human body, the swirling vortex of a hurricane, and even the spiral shapes of galaxies. In fact, we subconsciously attribute greater beauty to those whose faces more closely exhibit these proportions. This ratio seemed to be so deeply ingrained in the natural world that it quickly became known as the "Divine Proportion".
The precision with which these examples of naturally occurring Golden Ratios stick to the same proportion is astounding. It's no wonder many people attributed magical powers to this number.
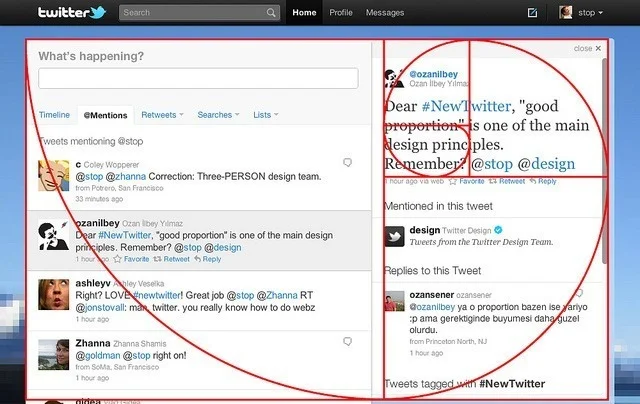
...You may even find the Golden Ratio in some unexpected places!
It wasn't long before people realized that not only are we surrounded by the Golden Ratio, but that it was aesthetically pleasing, well balanced, and incredibly strong. Throughout history humans have used this seemingly magical number to produce some of the most stunning and memorable works of architecture, art, and even music.
The Greeks were well known for incorporating Phi into much of their architecture. Not only is it visually balanced, but clearly it has withstood the test of time.
Many famous artists were well aware of the spacial laws of nature and, as a result, were able to create more realistic paintings.
Even in the world of music, using the numbers from the Fibonacci Sequence will yield favorable sounding proportions (the basis for musical scales and chords) that have been in use since monastic choral chanting all the way to today's pop music.
The use of Phi today
It's no wonder that the Golden Ratio continues to be used prolifically throughout modern society. Much of our technology, architecture, product design/ergonomics, and even the very web page you're reading this on have been heavily influenced by Phi.
If applied well, you won't notice the Golden Ratio because it simply "looks right" to our eyes. However, when misapplied or executed poorly, our brain will recognize it!
Clearly, there is much to be gained by incorporating these proportions into your own designs, but how do you go about it?
Finding a balance
When most people first learn about the Golden Ratio they have a tendency to use it in every aspect of a design. Every dimension, every line, every intersection has to be a reflection of Phi. Unfortunately, this inevitably leads to forced and often cluttered looking designs. While it is a useful tool, the Golden Ratio is not a panacea for bad design. Like everything else in life, there are often a multitude of variables that force us to establish certain limits on our work. Our use of φ can be best applied to filling in the aesthetic gaps left by these limiting factors.
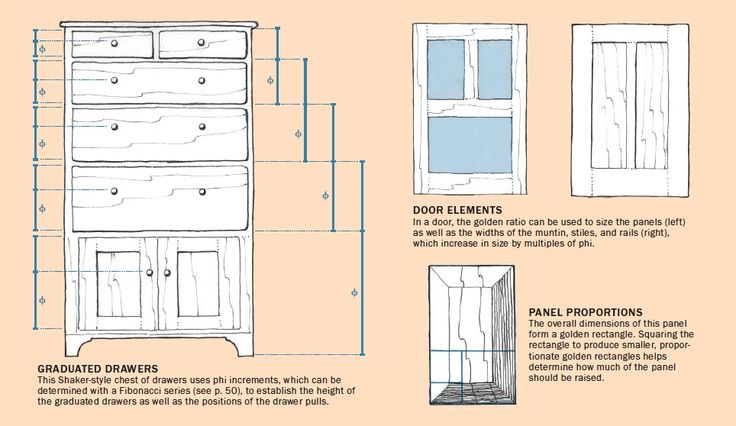
In terms of furniture design, we often start with one or more fixed dimensions. For example, in designing a hall table the height is commonly based on average human proportion so it will most likely be 30-32" tall. This is a fixed dimension that won't change. However, by applying the Golden Ratio I can come up with a proportionally balanced length. If my height is 30", the length would be derived as 30" x 1.618 = 48.54" which I would round to 48". Similarly, Phi can be used to give a more natural feel to graduated proportions such as drawers. Many people will graduate them using a fixed number, but I find that φ provides a balanced sense of motion to the piece.
While the drawers and doors are governed by φ, you'll notice that the overall height, width, and possibly depth may be limited by other factors such as available space or personal preference
These are just a few examples of incorporating the Golden Ratio into your designs. No matter the application- furniture, graphic design, art, photography- the key here is not to use Phi as a crutch. It's best to consider the limiting variables when planning a design so as to let it evolve naturally until you strike a good balance between form and function. Once you feel you have a solid foundation you can then go back and see where Phi can tweak some of the aesthetic proportions to help transform your design into something that is truly pleasing to the eye and balanced.
Dig Deeper
I hope this has been an informative introduction to the Golden Ratio and the Fibonacci Sequence. If you are truly interested in applying this ancient proportion to your work, I strongly suggest that you not only do further research on the subject, but put it into practice! Start to observe the objects that surround you, both natural and man-made. Practice breaking them down into their most basic lines and shapes and, more often than not, you'll find that φ is at the root of them. The building of this mental "Phi library" will help you to naturally incorporate it into your designs and art in such a way that your results will seem natural and elegant.
So that's it for now. As always, feel free to leave your comments and questions. I leave you now with some links to interesting tidbits to feed your ravenous curiosity. Until next time!